can be shown to take the following form for a spherical inclusion of the radius R (for more details see refs. [7, 8]):
V. I. Dubinko, Yu. T. Petrusenko, Kharkov Institute of Science and Technology
S. Goryachev, J. Foct, Laboratoire de Metallurgie Physique Universite de Lille, France
Zirconium belongs to the set of hexagonal close-packed metals where diffusion has been shown to be anisotropic. The diffusional anisotropy difference (DAD) between point defects changes the cavity bias for point defect absorption and leads to the depen dence of the dislocation bias on the distribution of dislocations in different crystallographic directions. This results in new critical quantities that control the transition from low-dose to high-dose irradiation effects such as the bubble-void transition and breakaway growth. In the present paper, a strong dependence of these critical quantities on DAD will be demonstrated that shows a need for further study of point defect diffusion in zirconium alloys. A combined approach is proposed for this purpose, which is based on computer simulations and on experimental investigations of intrinsic point defects. An electron accelerator is suggested for the investigation of the kinetics of accumulation and anneali ng of radiation defects in different grades of zirconium alloys. The method is based on measurement of the residual electric resistivity and recovery spectra of Zr samples irradiated with electrons at 4.2 K. Precise measurements of the activation energies of the main recovery stages will allow evaluation of the diffus ion activation energies of intrinsic point defects. Knowledge of the recovery stages and computer simulation results will be used for theoretical assessment of microstructural evolution in neutron irradiated zirconium. Anisotropic deformation ("growth") under irradiation of zirconium and its alloys has been the object of many experimental and theoretical studies [1-5]. However, the main microscopic mechanisms responsible for macroscopic growth are still a subject of debate. It is generally agreed that high growth rates (the so-called "break away" growth) correlate with appearance of c-component dislocations an d dislocation loops [2-5]. The c-component dislocations are considered to be net vacancy sinks due to diffusion anisotropy difference (DAD) between SIA’s and vacancies, the former migrating preferentially perpendicular to the c-axis [4, 6]. Their appearance would increase the total vacancy sink density from low level associated with grain boundaries alone, to a much higher level [3]. Because the c-component dislocations first appeared close to amorphous intermetallic inclusions, Holt and Gilbert [3] suggested that they could be generated by stresses resulting from differential dimensional changes of the inclusions a nd matrix during irradiation. Subsequent analysis has shown that these c-component dislocations were basal plane vacancy loops and that they first formed in volumes of increased solute concentration surrounding intermetallic particles [1]. More recently, Griffiths et al. [5] confirmed that the high growth rates are coincident with c-component loop formation on basal planes and with increase in the number density of small precipitates.
In the following section, we propose a quantitative description of a possible mechanism of the vacancy loop generation by second phase precipitates under irradiation, and show its dependence on DAD. In the subsequent section, computer models of point d efect in hcp metals are briefly reviewed and, finally, in section 3, an experimental verification of the models is discussed.
We will show briefly that the stresses required for a generation of a vacancy loop by a spherical inclusion can arise under irradiation due to accumulation of excess vacancies in the surrounding matrix, i.e. without any significant change of the inclus
ion size. This is possible as a result of the difference in diffusional influxes of radiation vacancies and SIA’s to the inclusion.
The net vacancy influx can be shown to take the following form for a spherical inclusion of the radius R (for more details see refs. [7, 8]):
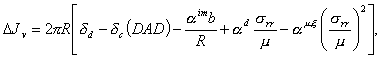 | (1) |
is the dislocation bias for SIA absorption,
is the bias of the cavity (where the inclusion is inserted) for SIA absorption due to DAD, dimensionless constants
having the upper scripts are the material constants corresponding to the different modes of elastic interaction between the inclusion and point defects [7, 8],
is the normal stress at the inclusion boundary, b is the interatomic spacing, and
is the shear modulus.
For an initially stress free inclusion (prior to irradiation) one has
, and according to Eq. (1), its cavity absorbs an excess of vacancies and start to grow in size if R > Rc, where Rc is the critical inclusion radius given by
 | (2) |
that increases the cavity bias for SIA absorption and, hence, decreases the excess vacancy influx until it vanishes at some stress value. In this case, the inclusion would absorb equal numbers of vacancies and SIA’s and act as an additional recombination
center for radiation point defects.
However, such equilibrium state can be stable only if the corresponding stress is lower than the threshold value
, above which the stress relaxation occurs via the production of a dislocation loop of vacancy type in the surrounding matrix [9]
 | (3) |
Thus, precipitates of certain sizes can transform diffusion influxes of radiation produced vacancies into outfluxes of vacancy loops (V-loops) resulting in the break away growth of the material.
Substituting the threshold stress value in Eq. (1) and setting the right-hand side equal to zero we obtain an expression for the threshold precipitate radius, Rth, below which precipitates are additional recombination centers whereas above R th, they can generate V-loops:
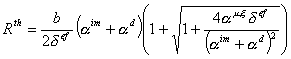 | (4) |
 | (5) |
The mean dislocation bias for SIA absorption depends on DAD and on the distribution of dislocations among the angles they have with c-axis, 
:
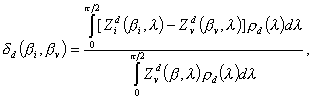 | (6) |
is the diffusion anisotropy parameter,
and 
are the principal values of the diffusion tensor along and orthogonal to c-axis. The dislocation capture efficiency is given by [9]
 | (7) |
is the capture efficiency in the isotropic case,
= 1, for which the dislocation bias is defined as
.
Below we will consider two dislocation types, namely, a-type dislocations with = 0 and c-type dislocations with = ¶/2.
An account of DAD can influence the irradiation behavior of materials very strongly depending on the diffusion anisotropy parameters and on the ratio of the dislocation densities with a-type and c-type Burgers vectors,
.
This is evident from Fig. 1, which shows the dependence of Rth on DAD that is defined as the difference:
.
DAD is positive if SIA’s diffusion anisotropy is stronger than that of vacancies, and negative in the opposite case. The former case is expected in the majority of hcp metals with less than ideal c/a ratios, including Zr, where there is increasing evidenc
e that vacancy migration is only weakly anisotropic, and SIAs migrate preferably in the basal plane [4, 6].
Based on this trend and on the observed prevalence of a-type dislocations in unirradiated zirconium (the curve a in Fig. 1),
the threshold precipitate size is expected to be small. That would explain the correlation of c-component loop formation on basal planes with increase in the number density of small precipitates [5].
However, computer modeling of point defects in Zr briefly reviewed in the following section gives controversial results depending on the calculation scheme and the choice of interatomic potential.
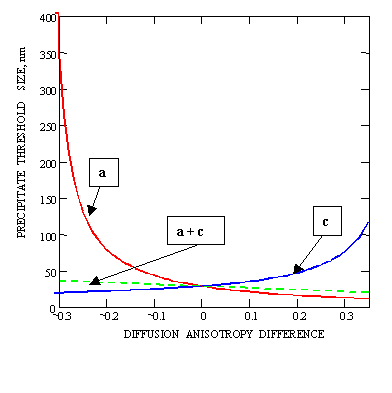
Dependence of precipitate threshold size, Rth, on DAD defined as the difference:
, at the following dislocation ratios and material parameters:
= ¥ (a);
= 1 (a+c);
= 0 (c).
,
,
,
.
Previous computer modeling of point defects in hcp metals has used simple pairwise interatomic potentials, which are not really adequate for simulating a metal as disparate as zirconium [10]. They were satisfactory for c/a close to ideal, however, and were in agreement with an increase in DAD with temperature observed in Zr [4]. This enhancement can be explained by a two-interstitial model with different contributions of the two interstitial states dominating at low (320K) and high (570 K) temperatures. The low temperature state were shown to be meta-stable and migrate preferentially along c-axis, and the stable high-temperature state migrated in the basal plane. More recently, Fernandez et al. [11] have used many-body potential based on the embedded atom method (EAM). This potential predicted rather strong vacancy migration anisotropy in Zr and SIA migration paths different from those predicted using pair potentials. As a result, DAD was predicted to decrease with increasing temperature and even to become negative abov e 520 K.
This controversy shows a need for using more realistic interatomic potentials such as those including angular dependence in the interactions. The influence of alloying additions and impurities on the point defect diffusion is of particular interest because of very significant effects observed experimentally. For example, for electron irradiated Zr-2.5Nb, there was no observable c-dislocation loop formation for doses up to about 5 dpa at 300 and 573 K [4]. The reason for it may be related to a decrease in DAD due to a high binding energy between Nb and Zr self-interstitial atoms.
It is evident from the above that there is a clear need for more experimental results concerning defect basic properties that could verify theoretical models. To the authors’ knowledge, there have been no experimental results that correlate the annealing phenomena in irradiated zirconium with interstitial configurations.
Irradiation facility "CRYOS" is suggested for the investigation of the kinetics of accumulation and annealing of radiation defects in different grades of zirconium alloys. It includes:
The method is based on measurement of the residual electric resistivity and recovery spectra of Zr samples irradiated with electrons at 4.2 K.
Precise measurements of the activation energies of the main recovery stages will allow evaluation of the diffusion activation energies of intrinsic point defects. Knowledge of the recovery stages and computer simulation results are required for theoretic
al assessment of microstructural evolution in neutron irradiated zirconium.
References